[1]   Scott Aaronson: P 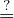NP. In John Forbes Nash, Jr. and Michael Th. Rassias, editors, Open Problems in Mathematics, pp. 1–122. Springer, 2016. [doi:10.1007/978-3-319-32162-2_1]

[2]   Scott Aaronson: P 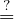NP. Electron. Colloq. Comput. Complexity, TR17-004, 2017. [ECCC]

[3]   Alexander Alder: Grenzrang und Grenzkomplexität aus algebraischer und topologischer Sicht. Ph. D. thesis, Zurich University, 1984.

[4]   Eric Allender and Fengming Wang: On the power of algebraic branching programs of width two. Comput. Complexity, 25(1):217–253, 2016. [doi:10.1007/s00037-015-0114-7]

[5]   Walter Baur and Volker Strassen: The complexity of partial derivatives. Theoret. Comput. Sci., 22(3):317–330, 1983. [doi:10.1016/0304-3975(83)90110-X]

[6]   Michael Ben-Or and Richard Cleve: Computing algebraic formulas using a constant number of registers. SIAM J. Comput., 21(1):54–58, 1992. [doi:10.1137/0221006]

[7]   Dario Bini, Milvio Capovani, Grazia Lotti, and Francesco Romani: O(n^2.7799) complexity for n × n matrix multiplication. Inform. Process. Lett., 8(5):234–235, 1979. [doi:10.1016/0020-0190(79)90113-3]

[8]   Markus Bläser: Lower bounds for the bilinear complexity of associative algebras. Comput. Complexity, 9(2):73–112, 2000. [doi:10.1007/PL00001605]

[9]   Markus Bläser: Complete problems for Valiant’s class of qp-computable families of polynomials. In Proc. 7th Internat. Combinatorics and Computing Conf. (COCOON’01), pp. 1–10. Springer, 2001. [doi:10.1007/3-540-44679-6_1]

[10]   Markus Bläser: Fast Matrix Multiplication. Number 5 in Graduate Surveys. Theory of Computing Library, 2013. [doi:10.4086/toc.gs.2013.005]

[11]   Markus Bläser and Christian Ikenmeyer: Lecture notes for Geometric Complexity Theory 2 (unpublished). Available at U. Warwick.

[12]    Markus Bläser, Christian Ikenmeyer, Gorav Jindal, and Vladimir Lysikov: Generalized matrix completion and algebraic natural proofs. In Proc. 50th STOC, pp. 1193–1206. ACM Press, 2018. [doi:10.1145/3188745.3188832]

[13]   Markus Bläser, Christian Ikenmeyer, Meena Mahajan, Anurag Pandey, and Nitin Saurabh: Algebraic branching programs, border complexity, and tangent spaces. In Proc. 35th Comput. Complexity Conf. (CCC’20), pp. 21:1–24. Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik, 2020. [doi:10.4230/LIPIcs.CCC.2020.21]

[14]   Richard P. Brent: The parallel evaluation of general arithmetic expressions. J. ACM, 21(2):201–206, 1974. [doi:10.1145/321812.321815]

[15]   Karl Bringmann, Christian Ikenmeyer, and Jeroen Zuiddam: On algebraic branching programs of small width. J. ACM, 65(5):32:1–29, 2018. [doi:10.1145/3209663]

[16]   Peter Bürgisser: Kombinatorik der Darstellungstheorie symmetrischer Gruppen (Combinatorics of the representation theory of symmetric groups). Course held in 2006 at Paderborn University. Handwritten course notes by Christian Ikenmeyer, unpublished.

[17]   Peter Bürgisser: Completeness and Reduction in Algebraic Complexity Theory. Springer, 2000. [doi:10.1007/978-3-662-04179-6]

[18]   Peter Bürgisser, Matthias Christandl, and Christian Ikenmeyer: Even partitions in plethysms. J. Algebra, 328(1):322–329, 2011. [doi:10.1016/j.jalgebra.2010.10.031]

[19]   Peter Bürgisser, Michael Clausen, and M. Amin Shokrollahi: Algebraic Complexity Theory. Springer, 1997. [doi:10.1007/978-3-662-03338-8]

[20]   Peter Bürgisser and Christian Ikenmeyer: Geometric complexity theory and tensor rank. In Proc. 43rd STOC, pp. 509–518. ACM Press, 2011. [doi:10.1145/1993636.1993704]

[21]   Peter Bürgisser and Christian Ikenmeyer: Explicit lower bounds via geometric complexity theory. In Proc. 45th STOC, pp. 141–150. ACM Press, 2013. [doi:10.1145/2488608.2488627]

[22]   Peter Bürgisser and Christian Ikenmeyer: Fundamental invariants of orbit closures. J. Algebra, 477:390–434, 2017. [doi:10.1016/j.jalgebra.2016.12.035]

[23]   Peter Bürgisser, Christian Ikenmeyer, and Greta Panova: No occurrence obstructions in geometric complexity theory. J. AMS, 32(1):163–193, 2019. Preliminary version in FOCS’16. [doi:10.1090/jams/908]

[24]   Peter Bürgisser, Joseph M. Landsberg, Laurent Manivel, and Jerzy Weyman: An overview of mathematical issues arising in the geometric complexity theory approach to VP ≠ VNP. SIAM J. Comput., 40(4):1179–1209, 2011. [doi:10.1137/090765328]

[25]   Prasad Chaugule, Nutan Limaye, and Shourya Pandey: Variants of the determinant polynomial and VP-completeness. In Proc. 16th Comp. Sci. Symp. in Russia (CSR’21), pp. 31–55. Springer, 2021. [doi:10.1007/978-3-030-79416-3_3]

[26]   Xi Chen, Neeraj Kayal, and Avi Wigderson: Partial derivatives in arithmetic complexity and beyond. Found. Trends Theor. Comp. Sci., 6(1–2):1–138, 2011. [doi:10.1561/0400000043]

[27]   Stephen Cook: The P versus NP problem. In The Millennium Prize Problems. Clay Mathematical Institute and American Mathematical Society, 2000. Available at AMS Bookstore.

[28]   Don Coppersmith and Shmuel Winograd: On the asymptotic complexity of matrix multiplication. SIAM J. Comput., 11(3):472–492, 1982. [doi:10.1137/0211038]

[29]   Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein: Introduction to Algorithms. MIT Press, 3rd edition, 2009.

[30]   László Csánky: Fast parallel matrix inversion algorithms. SIAM J. Comput., 5(4):618–623, 1976. [doi:10.1137/0205040]

[31]   Arnaud Durand, Meena Mahajan, Guillaume Malod, Nicolas de Rugy-Altherre, and Nitin Saurabh: Homomorphism polynomials complete for VP. Chicago J. Theoret. Comp. Sci., 2016(3), 2016. Preliminary version in FSTTCS’14.

[32]   Klim Efremenko, Ankit Garg, Rafael Oliveira, and Avi Wigderson: Barriers for rank methods in arithmetic complexity. In Proc. 9th Innovations in Theoret. Comp. Sci. Conf. (ITCS’18), pp. 1:1–19. Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik, 2018. [doi:10.4230/LIPIcs.ITCS.2018.1]

[33]   Ismor Fischer: Sums of like powers of multivariate linear forms. Math. Magazine, 67(1):59–61, 1994. [doi:10.2307/2690560]

[34]   Lance Fortnow: The status of the P versus NP problem. Commun. ACM, 52(9):78–86, 2009. [doi:10.1145/1562164.1562186]

[35]   Georg Ferdinand Frobenius: Über die Darstellung der endlichen Gruppen durch lineare Substitutionen. Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften zu Berlin, pp. 994–1015, 1897. [doi:10.3931/e-rara-18879]

[36]   William Fulton: Young Tableaux. Cambridge Univ. Press, 1996. [doi:10.1017/CBO9780511626241]

[37]   Ankit Garg, Visu Makam, Rafael Oliveira, and Avi Wigderson: More barriers for rank methods, via a “numeric to symbolic” transfer. In Proc. 60th FOCS, pp. 824–844. IEEE Comp. Soc., 2019. [doi:10.1109/FOCS.2019.00054]

[38]   David A. Gay: Characters of the Weyl group of SU(n) on zero weight spaces and centralizers of permutation representations. Rocky Mountain J. Math., 6(3):449–455, 1976. JSTOR.

[39]   Dima Grigoriev, Mikhail Muzychuk, and Ilya Ponomarenko: Tensor rank: Matching polynomials and Schur rings. Found. Computational Math., 14(3):457–481, 2014. [doi:10.1007/s10208-014-9190-3]

[40]   Joshua A. Grochow: Symmetry and equivalence relations in classical and geometric complexity theory. Ph. D. thesis, Department of Computer Science, University of Chicago, 2012. Available at author’s website.

[41]   Joshua A. Grochow: Unifying known lower bounds via geometric complexity theory. Comput. Complexity, 24(2):393–475, 2015. [doi:10.1007/s00037-015-0103-x]

[42]   Joshua A. Grochow, Ketan D. Mulmuley, and Youming Qiao: Boundaries of VP and VNP. In Proc. 43rd Internat. Colloq. on Automata, Languages, and Programming (ICALP’16), pp. 34:1–14. Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik, 2016. [doi:10.4230/LIPIcs.ICALP.2016.34]

[43]   Johan Håstad: Tensor rank is NP-complete. J. Algorithms, 11(4):644–654, 1990. [doi:10.1016/0196-6774(90)90014-6]

[44]   Roger Howe: (GL_n,GL_m)-duality and symmetric plethysm. Proc. Indian Acad. Sci. Math. Sci., 97(1–3):85–109, 1987. [doi:10.1007/BF02837817]

[45]   Jesko Hüttenhain and Pierre Lairez: The boundary of the orbit of the 3-by-3 determinant polynomial. C. R. Math. Acad. Sci. Paris, 354(9):931–935, 2016. [doi:https://doi.org/10.1016/j.crma.2016.07.002]

[46]   Christian Ikenmeyer: Geometric Complexity Theory, Tensor Rank, and Littlewood-Richardson Coefficients. Ph. D. thesis, Institute of Mathematics, University of Paderborn, 2012. Online available at U. Paderborn.

[47]   Christian Ikenmeyer and Greta Panova: Rectangular Kronecker coefficients and plethysms in geometric complexity theory. Adv. Math., 319:40–66, 2017. Preliminary version in FOCS’16. [doi:10.1016/j.aim.2017.08.024]

[48]   Harlan Kadish and Joseph M. Landsberg: Padded polynomials, their cousins, and geometric complexity theory. Comm. Algebra, 42(5):2171–2180, 2014. [doi:10.1080/00927872.2012.758268]

[49]   Allen Knutson: Peter-Weyl vs. Schur-Weyl theorem. MathOverflow post: https://mathoverflow.net/questions/267552/peter-weyl-vs-schur-weyl-theorem, 2017.

[50]   Emmanuel Kowalski: An Introduction to the Representation Theory of Groups. Amer. Math. Soc., 2014. [doi:10.1090/gsm/155]

[51]   Hanspeter Kraft: Geometrische Methoden in der Invariantentheorie. Friedr. Vieweg und Sohn Verlagsgesellschaft, Braunschweig, 1985. [doi:10.1007/978-3-322-83813-1]

[52]   Joseph M. Landsberg: New lower bounds for the rank of matrix multiplication. SIAM J. Comput., 43(1):144–149, 2014. [doi:10.1137/120880276]

[53]   Joseph M. Landsberg: Geometric complexity theory: an introduction for geometers. Annali dell’ Università di Ferrara, 61(1):65–117, 2015. [doi:10.1007/s11565-014-0202-7]

[54]   Joseph M. Landsberg: Geometry and Complexity Theory. Cambridge Univ. Press, 2017. [doi:10.1017/9781108183192]

[55]   Joseph M. Landsberg, Laurent Manivel, and Nicolas Ressayre: Hypersurfaces with degenerate duals and the Geometric Complexity Theory Program. Comment. Math. Helvetici, 88(2):469–484, 2013. [doi:10.4171/CMH/292]

[56]   Joseph M. Landsberg and Mateusz Michałek: A 2n² - log ₂(n) - 1 lower bound for the border rank of matrix multiplication. Internat. Math. Research Notices, 2018(15):4722–4733, 2018. [doi:10.1093/imrn/rnx025]

[57]   Joseph M. Landsberg and Giorgio Ottaviani: New lower bounds for the border rank of matrix multiplication. Theory of Computing, 11(11):285–298, 2015. [doi:10.4086/toc.2015.v011a011]

[58]   Michael J. Larsen and Richard Pink: Determining representations from invariant dimensions. Inventiones Math., 102(2):377–398, 1990. [doi:10.1007/BF01233432]

[59]   Meena Mahajan and Nitin Saurabh: Some complete and intermediate polynomials in algebraic complexity theory. Theory Computing Sys., 62(3):622–652, 2018. [doi:10.1007/s00224-016-9740-y]

[60]   Meena Mahajan and V. Vinay: Determinant: Combinatorics, algorithms, and complexity. Chicago J. Theoret. Comp. Sci., 1997(5), 1997. [doi:10.4086/cjtcs.1997.005]

[61]   Guillaume Malod and Natacha Portier: Characterizing Valiant’s algebraic complexity classes. J. Complexity, 24(1):16–38, 2008. [doi:10.1016/j.jco.2006.09.006]

[62]   Ketan D. Mulmuley: On P vs. NP and geometric complexity theory: Dedicated to Sri Ramakrishna. J. ACM, 58(2):5:1–26, 2011. [doi:10.1145/1944345.1944346]

[63]   Ketan D. Mulmuley and Milind Sohoni: Geometric complexity theory. I. An approach to the P vs. NP and related problems. SIAM J. Comput., 31(2):496–526, 2001. [doi:10.1137/S009753970038715X]

[64]    Ketan D. Mulmuley and Milind Sohoni: Geometric complexity theory II: Towards explicit obstructions for embeddings among class varieties. SIAM J. Comput., 38(3):1175–1206, 2008. [doi:10.1137/080718115]

[65]   David B. Mumford: Algebraic Geometry I: Complex Projective Varieties. Classics in mathematics. Springer, 1995. Reprint of the 1976 edition in Grundlehren der mathematischen Wissenschaften, vol. 221. Available at Springer.

[66]   Kyo Nishiyama: Restriction of the irreducible representations of GL_n to the symmetric group S_n. Unpublished preprint, online available at Kyoto University.

[67]   Alexander Ostrowski: On two problems in abstract algebra connected with Horner’s rule. In Studies in Mathematics and Mechanics presented to Richard von Mises, pp. 40–48. Academic Press, 1954. [doi:10.1016/B978-1-4832-3272-0.50010-7]

[68]   Kenneth W. Regan: Understanding the Mulmuley–Sohoni approach to P vs NP. Bulletin of the EATCS, 78:86–99, 2002. Available at author’s website.

[69]   Jeffrey B. Remmel: A formula for the Kronecker products of Schur functions of hook shapes. J. Algebra, 120(1):100–118, 1989. [doi:10.1016/0021-8693(89)90191-9]

[70]   Mercedes H. Rosas: The Kronecker product of Schur functions indexed by two-row shapes or hook shapes. J. Algebraic Combinatorics, 14(2):153–173, 2001. [doi:10.1023/A:1011942029902]

[71]   Marcus Schaefer and Daniel Štefankovič: The complexity of tensor rank. Theory Computing Sys., 62(5):1161–1174, 2018. [doi:10.1007/s00224-017-9800-y]

[72]   Yaroslav Shitov: How hard is tensor rank?, 2016. [arXiv:1611.01559]

[73]   Zhao Song, David P. Woodruff, and Peilin Zhong: Relative error tensor low rank approximation. In Proc. 30th Ann. ACM–SIAM Symp. on Discrete Algorithms (SODA’19), pp. 2772–2789. SIAM, 2019. [doi:10.1137/1.9781611975482.172]

[74]   Richard P. Stanley: Positivity problems and conjectures in algebraic combinatorics. In Mathematics: Frontiers and perspectives, pp. 295–319. Amer. Math. Soc., 2000. Available at author’s website.

[75]   Volker Strassen: Gaussian elimination is not optimal. Numerische Mathematik, 13:354–356, 1969. [doi:10.1007/BF02165411]

[76]   Volker Strassen: Polynomials with rational coefficients which are hard to compute. SIAM J. Comput., 3(2):128–149, 1974. [doi:10.1137/0203010]

[77]   Volker Strassen: Relative bilinear complexity and matrix multiplication. J. reine angew. Math., 375–376(4):406–443, 1987. Available at EuDML.

[78]   Joseph Swernofsky: Tensor rank is hard to approximate. In Proc. 21st Internat. Conf. on Approximation Algorithms for Combinat. Opt. Probl. (APPROX’18), pp. 26:1–9. Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik, 2018. [doi:10.4230/LIPIcs.APPROX-RANDOM.2018.26]

[79]   Patrice Tauvel and Rupert W. T. Yu: Lie Algebras and Algebraic Groups. Springer, 2005. [doi:10.1007/b139060]

[80]   Leslie G. Valiant: Completeness classes in algebra. In Proc. 11th STOC, pp. 249–261. ACM Press, 1979. [doi:10.1145/800135.804419]

[81]    Leslie G. Valiant: The complexity of computing the permanent. Theoret. Comput. Sci., 8(2):189–201, 1979. [doi:10.1016/0304-3975(79)90044-6]

[82]   Leslie G. Valiant, Sven Skyum, Stuart J. Berkowitz, and Charles Rackoff: Fast parallel computation of polynomials using few processors. SIAM J. Comput., 12(4):641–644, 1983. [doi:10.1137/0212043]

[83]   Jun Yu: On the dimension datum of a subgroup. Duke Math. J., 165(14):2683–2736, 2016. [doi:10.1215/00127094-3619898]