A Constructive Lovász Local Lemma for Permutations
by David G. Harris and Aravind Srinivasan
Theory of Computing, Volume 13(17), pp. 1-41, 2017
Bibliography with links to cited articles
[1] Dimitris Achlioptas and Fotis Iliopoulos: Random walks that find perfect objects and the Lovász Local Lemma. J. ACM, 63(3):22:1–29, 2016. Preliminary version in FOCS’14. [doi:10.1145/2818352, arXiv:1406.0242]
[2] Ron Aharoni, Eli Berger, and Ran Ziv: Independent systems of representatives in weighted graphs. Combinatorica, 27(3):253–267, 2007. [doi:10.1007/s00493-007-2086-y]
[3] Michael H. Albert, Alan M. Frieze, and Bruce A. Reed: Multicoloured Hamilton cycles. Electr. J. Combin., 2(R10), 1995. URL.
[4] Noga Alon: Probabilistic proofs of existence of rare events. In Geometric Aspects of Functional Analysis, volume 1376 of Lect. Notes in Math., pp. 186–201. Springer, 1989. [doi:10.1007/BFb0090055]
[5] Noga Alon: The strong chromatic number of a graph. Random Structures Algorithms, 3(1):1–7, 1992. [doi:10.1002/rsa.3240030102]
[6] Noga Alon, László Babai, and Alon Itai: A fast and simple randomized parallel algorithm for the maximal independent set problem. J. Algorithms, 7(4):567–583, 1986. [doi:10.1016/0196-6774(86)90019-2]
[7] Noga Alon, Joel H. Spencer, and Prasad Tetali: Covering with Latin transversals. Discr. Appl. Math., 57(1):1–10, 1995. [doi:10.1016/0166-218X(93)E0136-M]
[8] Maria Axenovich and Ryan R. Martin: On the strong chromatic number of graphs. SIAM J. Discrete Math., 20(3):741–747, 2006. [doi:10.1137/050633056, arXiv:1605.06574]
[9] Rodrigo Bissacot, Roberto Fernández, Aldo Procacci, and Benedetto Scoppola: An improvement of the Lovász Local Lemma via cluster expansion. Combin. Probab. Comput., 20(5):709–719, 2011. [doi:10.1017/S0963548311000253, arXiv:0910.1824]
[10] Julia Böttcher, Yoshiharu Kohayakawa, and Aldo Procacci: Properly coloured copies and rainbow copies of large graphs with small maximum degree. Random Structures Algorithms, 40(4):425–436, 2012. [doi:10.1002/rsa.20383, arXiv:1007.3767]
[11] Stephen A. Cook: A taxonomy of problems with fast parallel algorithms. Inf. Control, 64(1-3):2–22, 1985. [doi:10.1016/S0019-9958(85)80041-3]
[12] Paul Erd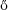 s, Dean R. Hickerson, Donald A. Norton, and Sherman K.
Stein: Has every Latin square of order n a partial Latin transversal of size
n - 1? Amer. Math. Monthly, 95(5):428–430, 1988. [doi:10.2307/2322477]
s, Dean R. Hickerson, Donald A. Norton, and Sherman K.
Stein: Has every Latin square of order n a partial Latin transversal of size
n - 1? Amer. Math. Monthly, 95(5):428–430, 1988. [doi:10.2307/2322477]
[13] Paul Erd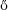 s and Joel H. Spencer: Lopsided Lovász Local Lemma
and Latin transversals. Discr. Appl. Math., 30(2-3):151–154, 1991.
[doi:10.1016/0166-218X(91)90040-4]
s and Joel H. Spencer: Lopsided Lovász Local Lemma
and Latin transversals. Discr. Appl. Math., 30(2-3):151–154, 1991.
[doi:10.1016/0166-218X(91)90040-4]
[14] Michael R. Fellows: Transversals of vertex partitions in graphs. SIAM J. Discrete Math., 3(2):206–215, 1990. [doi:10.1137/0403018]
[15] Alan M. Frieze and Michael Krivelevich: On rainbow trees and cycles. Electr. J. Combin., 15(R59), 2008. URL.
[16] Bernhard Haeupler, Barna Saha, and Aravind Srinivasan: New constructive aspects of the Lovász Local Lemma. J. ACM, 58(6):28:1–28, 2011. [doi:10.1145/2049697.2049702, arXiv:1001.1231]
[17] Geňa Hahn and Carsten Thomassen: Path and cycle sub-Ramsey numbers and an edge-colouring conjecture. Discrete Math., 62(1):29–33, 1986. [doi:10.1016/0012-365X(86)90038-5]
[18] David G. Harris and Aravind Srinivasan: The Moser-Tardos framework with partial resampling. In Proc. 54th FOCS, pp. 469–478. IEEE Comp. Soc. Press, 2013. [doi:10.1109/FOCS.2013.57, arXiv:1406.5943]
[19] David G. Harris and Aravind Srinivasan: A constructive algorithm for the Lovász Local Lemma on permutations. In Proc. 25th Ann. ACM-SIAM Symp. on Discrete Algorithms (SODA’14), pp. 907–925. ACM Press, 2014. [doi:10.1137/1.9781611973402.68, arXiv:1612.02663]
[20] Nicholas J. A. Harvey and Jan Vondrák: An algorithmic proof of the Lovász Local Lemma via resampling oracles. In Proc. 56th FOCS, pp. 1327–1346. IEEE Comp. Soc. Press, 2015. [doi:10.1109/FOCS.2015.85, arXiv:1504.02044]
[21] Penny E. Haxell: On the strong chromatic number. Combin. Probab. Comput., 13(6):857–865, 2004. [doi:10.1017/S0963548304006157]
[22] Penny E. Haxell: An improved bound for the strong chromatic number. J. Graph Theory, 58(2):148–158, 2008. [doi:10.1002/jgt.20300]
[23] A. Donald Keedwell and József Dénes: Latin Squares and Their Applications. 2nd ed. Elsevier, 2015.
[24] Peter Keevash and Cheng Yeaw Ku: A random construction for permutation codes and the covering radius. Designs, Codes and Cryptography, 41(1):79–86, 2006. [doi:10.1007/s10623-006-0017-3]
[25] Kashyap Babu Rao Kolipaka and Mario Szegedy: Moser and Tardos meet Lovász. In Proc. 43rd STOC, pp. 235–244. ACM Press, 2011. [doi:10.1145/1993636.1993669]
[26] Vladimir Kolmogorov: Commutativity in the algorithmic Lovász Local Lemma. In Proc. 57th FOCS, pp. 780–787. IEEE Comp. Soc. Press, 2016. [doi:10.1109/FOCS.2016.88, arXiv:1506.08547]
[27] Linyuan Lu, Austin Mohr, and László Székely: Quest for negative dependency graphs. In Recent Advances in Harmonic Analysis and Applications, pp. 243–258. Springer, 2012. [doi:10.1007/978-1-4614-4565-4_21]
[28] Linyuan Lu and László Székely: Using Lovász Local Lemma in the space of random injections. Electr. J. Combin., 14(R63), 2007. URL.
[29] Michael Luby: A simple parallel algorithm for the maximal independent set problem. SIAM J. Comput., 15(4):1036–1053, 1986. Preliminary version in STOC’85. [doi:10.1137/0215074]
[30] Austin Mohr: Applications of the lopsided Lovász Local Lemma regarding hypergraphs. Ph. D. thesis, University of South Carolina, 2013. Available at author’s webpage.
[31] Robin A. Moser and Gábor Tardos: A constructive proof of the general Lovász Local Lemma. J. ACM, 57(2):11:1–15, 2010. [doi:10.1145/1667053.1667060, arXiv:0903.0544]
[32] Wesley Pegden: An extension of the Moser-Tardos algorithmic local lemma. SIAM J. Discrete Math., 28(2):911–917, 2014. [doi:10.1137/110828290, arXiv:1102.2853]
[33] Alexander D. Scott and Alan D. Sokal: The repulsive lattice gas, the independent-set polynomial, and the Lovász Local Lemma. J. Stat. Phys., 118(5-6):1151–1261, 2005. [doi:10.1007/s10955-004-2055-4, arXiv:cond-mat/0309352]
[34] James B. Shearer: On a problem of Spencer. Combinatorica, 5(3):241–245, 1985. [doi:10.1007/BF02579368]
[35] Sherman K. Stein: Transversals of Latin squares and their generalizations. Pacific J. Math., 59(2):567–575, 1975. [doi:10.2140/pjm.1975.59.567]
[36] Sándor Szabó: Transversals of rectangular arrays. Acta Math. Univ. Comenianae, 77(2):279–284, 2008. Available at EMIS.
